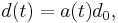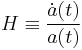Scale factor (cosmology)

The scale factor or cosmic scale factor parameter of the Friedmann equations is a function of time which represents the relative expansion of the universe. It is sometimes called the Robertson-Walker scale factor.[1] It is the (time-dependent) factor that relates the proper distance (which can change over time, unlike the comoving distance which is constant) for a pair of objects moving with the Hubble flow in an expanding or contracting FLRW universe—the distance between a pair of galaxies, for example—at any arbitrary time t to their distance at some reference time, generally taken to be the present, by the formula:

d(t) = a(t)d_0,\,

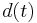where d(t) is the proper distance at epoch 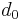t, d_0 is the distance at the reference time 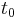t_0 (the present epoch), and 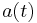a(t) is the scale factor.[2] Thus, by definition, a(t_0) = 1.

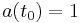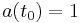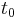The scale factor could, in principle, have units of length or be dimensionless. Most commonly in modern usage, it is chosen to be dimensionless, with the current value equal to one: a(t_0) = 1, where t is counted from the birth of the universe and t_0 is the present age of the universe: 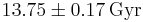13.75\pm0.17\,\mathrm{Gyr}.[3]

The evolution of the scale factor is a dynamical question, determined by the equations of general relativity, which are presented in the case of a locally isotropic, locally homogeneous universe by the Friedmann equations.

The Hubble parameter is defined:

H \equiv {\dot{a}(t) \over a(t)}

where the dot represents a time derivative. From the previous equation 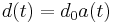d(t) = d_0 a(t) one can see that 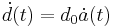\dot{d}(t) = d_0 \dot{a}(t), and also that 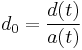d_0 = \frac{d(t)}{a(t)}, so combining these gives 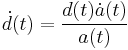\dot{d}(t) = \frac{d(t) \dot{a}(t)}{a(t)}, and substituting the above definition of the Hubble parameter gives 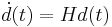\dot{d}(t) = H d(t) which is just Hubble's law.

Current evidence suggests that the expansion rate of the universe is accelerating, which means that the second derivative of the scale factor 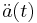\ddot{a}(t) is positive, or equivalently that the first derivative 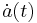\dot{a}(t) is increasing over time.[4] This also implies that any given galaxy recedes from us with increasing speed over time, i.e. for that galaxy 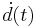\dot{d}(t) is increasing with time. In contrast, the Hubble parameter seems to be decreasing with time, meaning that if we were to look at some fixed distance d and watch a series of different galaxies pass that distance, later galaxies would pass that distance at a smaller velocity than earlier ones.[5]

According to the Friedmann–Lemaître–Robertson–Walker metric which is used to model the expanding universe, if at the present time we receive light from a distant object with a redshift of z, then the scale factor at the time the object originally emitted that light is given by the equation 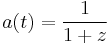a(t) = \frac{1}{1 %2B z}.[6][7]

See also

References

  1. ^ Steven Weinberg (2008). Cosmology. Oxford University Press. p. 3. ISBN 9780198526827. http://books.google.com/books?id=48C-ym2EmZkC&pg=PA3. 
  2. ^ Schutz, Bernard (2003). Gravity from the Ground Up: An Introductory Guide to Gravity and General Relativity. Cambridge University Press. p. 363. ISBN 978-0521455060. 
  3. ^ S. H. Suyu, P. J. Marshall, M. W. Auger, S. Hilbert, R. D. Blandford, L. V. E. Koopmans, C. D. Fassnacht and T. Treu. Dissecting the Gravitational Lens B1608+656. II. Precision Measurements of the Hubble Constant, Spatial Curvature, and the Dark Energy Equation of State. The Astrophysical Journal, 2010; 711 (1): 201 DOI: 10.1088/0004-637X/711/1/201
  4. ^ Jones, Mark H.; Robert J. Lambourne (2004). An Introduction to Galaxies and Cosmology. Cambridge University Press. p. 244. ISBN 978-0521837385. 
  5. ^ Is the universe expanding faster than the speed of light? (see final paragraph)
  6. ^ Davies, Paul (1992), The New Physics, p. 187.
  7. ^ Mukhanov, V. F. (2005), Physical Foundations of Cosmology, p. 58.

External links